APLICACIONES DERIVADA OPTIMIZACIÓN PARÁMETROS
APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS PARA MATEMÁTICAS DE BACHILLERATO. RECTA TANGENTE Y NORMAL A UNA CURVA. EJERCICIOS RESUELTOS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- TABLA DE DERIVADAS
- CURSO DE CÁLCULO DE DERIVADAS PARA BACHILLERATO
- CÁLCULO DE DERIVADAS PARA MATEMÁTICAS DE BACHILLERATO
- RECETA PARA ESTUDIAR CRECIMIENTO Y CURVATURA (CONCAVIDAD Y CONVEXIDAD) DE UNA FUNCIÓN, MÁXIMOS, MÍNIMOS Y PUNTOS DE INFLEXIÓN
- APLICACIONES DE LA DERIVADA: MONOTONÍA Y CURVATURA PARA MATEMÁTICAS DE BACHILLERATO. EJERCICIOS RESUELTOS
- TABLA DE DERIVADAS
INDICACIONES PARA RESOLVER PROBLEMAS DE OPTIMIZACIÓN:
-
- LEER TANTAS VECES EL EJERCICIO QUE CASI LO SEPAS DE MEMORIA!!!, ya que son en ocasiones difíciles de interpretar. Cuando el ejercicio de optimización consista en una situación relacionada con la geometría, dibujar la situación, poniendo nombre a cada uno de los elementos que intervienen en el ejercicio.
- Identificar la función objeto de máximo o mínimo (qué queremos que sea máximo o mínimo: superficie, volumen, distancia, tiempo….)
- Ponerla en función de una sola variable, utilizando los datos del problema. (ojo que a veces es mejor una variable que la otra a la hora de derivar)
- Una vez la función objeto de máximo o mínimo está en función de una sola variable, derivarla e igualarla a cero. Al resolver esta ecuación tenemos los posibles Máximos o mínimos.
- Confirmar el máximo o mínimo:
- LEER TANTAS VECES EL EJERCICIO QUE CASI LO SEPAS DE MEMORIA!!!, ya que son en ocasiones difíciles de interpretar. Cuando el ejercicio de optimización consista en una situación relacionada con la geometría, dibujar la situación, poniendo nombre a cada uno de los elementos que intervienen en el ejercicio.
Si la segunda derivada es fácil de calcular, sustituir los posibles máximos o mínimos en la segunda derivada (Recordar que si al sustituir es negativa tenemos un Máximo y si positiva mínimo)
Si es complicado el cálculo de la segunda, utilizar la primera derivada, sustituyendo un punto por encima y otro por debajo del posible máximo o mínimo y recordar que antes de un máximo la función es creciente (1ª derivada positiva) y después decreciente (1ª derivada negativa). En un mínimo antes es exactamente lo contrario: decreciente primero y después creciente.
EJERCICIO M2BE3462: (EBAU CANARIAS JULIO 2018)
Tenemos que hacer dos cuadrados de tela y cada cuadrado con una tela diferente.
Las dos telas tienen precios de 2 y 3 euros por centímetro cuadrado respectivamente.
¿Cómo hemos de elegir los lados de los cuadrados si queremos que el coste total sea mínimo y si además nos piden que la suma de los perímetros de los dos cuadrados ha de ser 100 cm?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3462, PROBLEMA DE OPTIMIZACIÓN. EBAU CANARIAS JULIO 2018
EJERCICIO M2BE2163, EBAU Canarias 2017:
Se quiere fabricar un smartphone con una pantalla LCD de 18 cm2. Los bordes superior e inferior han de tener 2 cm cada uno y los bordes laterales 1 cm. Calcular las dimensiones del teléfono para que la superficie del mismo sea mínima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/Us6K799tABA
EJERCICIO M2BE2164:
Se quiere construir una ventana rectangular de 1 metro cuadrado de área. El coste del marco es de 12.5 euros por cada metro de altura y de 8 euros por cada metro de anchura. ¿Qué dimensiones debe tener la ventana para que el marco resulte lo más económico posible?
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/ZOYcoL5CytU
EJERCICIO M2BE2099:
Se tiene un alambre de 1 metro de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/90cVkMM1tXY
EJERCICIO M2BE2239: EBAU CANARIAS JUNIO 2013
La figura siguiente muestra un rombo inscrito dentro de un rectángulo, de forma que los vértices del rombo se sitúan en los puntos medios de los lados del rectángulo. El perímetro del rectángulo es de 100 metros. Calcular las longitudes de sus lados para que el área del rombo inscrito sea máxima.
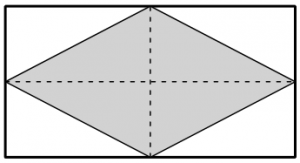
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2239, PROBLEMA DE OPTIMIZACIÓN EBAU CANARIAS JUNIO 2013
EJERCICIO M2BE2100:
Dividir un segmento de 6 cm de longitud en dos partes, con la propiedad de que la suma de las áreas del cuadrado y del triángulo equilátero construidos sobre ellos sea máxima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/UZpwBucitbk
EJERCICIO M2BE1955:
En una circunferencia de 20 cm de diámetro deseamos inscribir un rectángulo. Hallar las dimensiones del que tenga el área mayor. Razonar el proceso seguido, utilizando las herramientas matemáticas apropiadas que no dejen lugar a duda del resultado obtenido.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/P4d3rc87yUA
EJERCICIO M2BE1957:
Un nadador se encuentra en la playa de Las Canteras, a 700 m de la orilla, justo enfrente de la torre de la Cruz Roja. Desea ir a un punto situado a 1400 m de la torre, donde dejó a su pareja. Como observa que su pareja lo está llamando para comer, quiere llegar a la misma lo antes posible. El nadador sabe que nada a 2.5 km/h y que corre a 3 km/h. Indicar al nadador a qué punto entre la torre de la Cruz Roja y su toalla debe dirigirse, si quiere llegar en el menor tiempo posible, no sea que su pareja se acabe la ensaladilla rusa.
VÍDEO DONDE SE RESUELVE EL EJERCICIO: https://youtu.be/55T1kumaCJY
EJERCICIO M2BE2221:
Se dispone de un hilo metálico de longitud 140 m. Se quiere dividir dicho hilo en tres trozos de forma que la longitud de uno de los trozos sea el doble de la longitud de otro y tal que, al construir con cada uno de los tres trozos de hilo un cuadrado, la suma de las áreas de los tres cuadrados sea mínima. Encontrar la longitud de cada trozo.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN FINAL GLOBAL MATEMÁTICAS 2º BACHILLERATO
EJERCICIO M1BE2481:
Dos postes con longitudes de 6 y 8 metros respectivamente se colocan verticalmente sobre el piso con sus bases separadas una distancia de 10 metros. Calcula aproximadamente la longitud mínima de un cable que pueda ir desde la punta de uno de los postes hasta un punto en el suelo entre los postes y luego hasta la punta del otro poste.
EJERCICIO M2BE1521, DE CÁLCULO DE PARÁMETROS:
Dada la función f(x) = ax2+ bx + c , determinar los valores de a , b y c para que se cumpla: que la gráfica de f(x) pase por el punto (0, 4) y que la recta y = – 4x + 7 sea tangente a la gráfica de f (x) en el punto de abscisa x = 1.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/13pDHPgLvtU
OTRO VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/hH5gaOV6CrY
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO EN FORMATO TEXTO: EJERCICIOS RESUELTOS DE EXAMEN. ANÁLISIS DE FUNCIONES PARA 1º DE BACHILLERATO. TERCER TRIMESTRE CURSO 2024-25
EJERCICIO M1BE2027:
Determinar los valores de a, b y c sabiendo que la función f(x) = x3+ax2+bx+c , tiene extremos relativos en x=1 y x=-3, y que corta a su función derivada en x=0. Determinar asimismo la naturaleza de los extremos.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/UddHOBnzfRU
EJERCICIO M1BE2028:
Determinar una función de la forma f(x) = x3+ax2+bx+c ,que tenga un extremo relativo en el punto de abscisa x=2 y para la cual el punto P(1, 2) sea un punto de inflexión.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/z5oCkg4bWTQ
EJERCICIO M2BE2102:
Sea f(x) = x4 + ax2 + bx + c . Obtener a, b y c para que en el punto de abscisa x=0, la recta la tangente a la gráfica de f(x) sea y = 2x – 1 , y en el punto de abscisa x=1 la recta tangente a la gráfica de f sea horizontal.
El extremo situado en el punto de abscisa x=1 ¿es máximo o mínimo?
IR A LA RESOLUCIÓN DE ESTE EJERCICIO EN: EXAMEN BLOQUE ANÁLISIS MATEMÁTICAS II. 2º BACHILLERATO
EJERCICIO M2BE2315, EBAU CANARIAS 2019-20 EXTRAORDINARIA:
Hallar los valores de a y b para que la recta de ecuación y=6x+a sea tangente a la curva f(x), en el punto de abscisa x=0, siendo f(x):
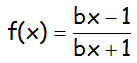
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO
EJERCICIO M2BE2355:
Considera la función f(x) = ax3 + bx2 + cx + d.
Calcular los coeficientes a, b, c y d, sabiendo que f tiene un extremo relativo en el punto P(0,1) y su gráfica tiene un punto de inflexión Q(1, -1).
Dar la expresión de la función f(x).
IR A LA RESOLUCIÓN DE ESTE EJERCICIO DE CÁLCULO DE PARÁMETROS
EJERCICIO M2BE3386:
Para la siguiente función f(x):
![]()
Calcular el dominio y los extremos relativos.
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA INTEGRAL: EXAMEN RESUELTO BLOQUE ANÁLISIS FUNCIONES. MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 3 DEL PRIMER TRIMESTRE 2025-26.
EJERCICIO M2BE3387:
Para la siguiente función f(x):
![]()
Calcula la recta tangente en x = 1 .
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA INTEGRAL: EXAMEN RESUELTO BLOQUE ANÁLISIS FUNCIONES. MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 3 DEL PRIMER TRIMESTRE 2025-26.
EJERCICIO M1BE2029:
Se sabe que la gráfica de la función siguiente f(x):
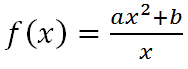
tiene una recta tangente horizontal en el punto P(2, 4). Hallar los valores de a y b.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/KVSzz4y0xoQ
EJERCICIO M2BE2607:
Dada la siguiente función f(x):

Se pide:
a) Determinar la recta tangente y normal en x = 0.
b) Calcular los máximos y mínimos relativos.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II DE 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES PRIMER TRIMESTRE 2024-25
EJERCICIO M1BE2446:
Considerar la función f(x) = ax3 + bx2 + cx + d.
Hallar los coeficientes a, b, c y d sabiendo que f tiene un extremo relativo en el punto P (0,1) y que su gráfica tiene un punto de inflexión Q (-1,1).
EJERCICIO M1BE2447:
Sea f(x) = x4 + ax2 + bx + c. Obtener a, b y c para que en el punto de abscisa x=0, la recta tangente a la gráfica de f(x) sea y = 2x -1, y en el punto de abscisa x = 1 la recta tangente a la gráfica de f sea horizontal.
El extremo situado en el punto de abscisa x=1 ¿es máximo o mínimo?.
EJERCICIO M1BE2448:
Determinar una función de la forma f(x) = x3 + ax2 + bx + c , que tenga un extremo relativo en el punto de abscisa x=2 y para la cual el punto P (1,2) sea un punto de inflexión.
EJERCICIO M1BE2449:
Calcular el valor de los parámetros c y d sabiendo que la gráfica de la función definida por f(x) = 2x3 -x2 +cx +d, tiene como recta tangente en el punto P (1, -2) la recta de ecuación y = 5x – 7.
EJERCICIO M1BE2450:
Dada la función f(x) = x4 +ax3 + bx2 + cx + 7 :
Calcular los valores de a, b y c, sabiendo que se cumplen las condiciones siguientes:
- Dos de sus extremos relativos se encuentran en los puntos de abscisa x=0 y x=-2.
- La función corta el eje OX en el punto x=1.
Dar la expresión de la función resultante.
EJERCICIO M1BE2451: (EBAU CANARIAS JULIO 2018)
Determinar los valores de a y b para que la función f(x) determinada por:
![]()
tenga un punto de inflexión en el punto (2, 8).
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE2451, DE CÁLCULO DE PARÁMETROS COMO APLICACIÓN DE LA DERIVADA. EBAU CANARIAS JULIO 2018
EJERCICIO M1BE2453:
Dada la función f(x) = ax2 + bx + c , determinar los valores de a, b y c para que se cumplan las siguientes condiciones:
- Que la gráfica de f(x) pase por el punto (0, 4).
- Que la recta y = -4x + 7 sea tangente a la gráfica de f(x) en el punto de abscisa x=1.
EJERCICIO M1BE2454:
Determinar una función f(x) = ax3 + bx2 + cs + d , sabiendo que su gráfica pasa por el punto P(-1,2) y tiene un punto de inflexión con tangente horizontal en Q(0, -2).
EJERCICIO M2BE1998 B:
Dividir un segmento de 6 cm de longitud en dos partes, con la propiedad de que la suma de las áreas del cuadrado y del triángulo equilátero construidos sobre ellos sea máxima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/UZpwBucitbk
EJERCICIO M2BE2162:
Se quiere construir una ventana rectangular de 2 metros cuadrados de área. El coste del marco es de 15 euros por cada metro de altura y de 10 euros por cada metro de anchura. ¿Qué dimensiones debe tener la ventana para que el marco resulte lo más económico posible?
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN GEOMETRÍA, ÁLGEBRA, ANÁLISIS PARA MATEMÁTICAS 2º BACHILLERATO
DERIVADAS EN FÍSICA:
La derivada es variación. Los conceptos que se trabajan en física en bachillerato, pueden servir para intentar entender la importancia de la derivada como herramienta matemática aplicada en Física. Les proponemos el siguiente material audiovisual, que puede ser de interés para ver la utilidad de esta herramienta.
EJERCICIO M2BE2131:
Dada la función:
![]()
a.- Determina los valores de los parámetros para que dicha función tenga un extremo relativo en el punto de abscisa x=3, y además pase por el punto (1,-1/e)
b.- Halla la ecuación de la recta tangente a f(x) en el punto de abscisa x=0.
IR AL ARTÍCULO CON LA SOLUCIÓN DEL ESTE EJERCICIO Y OTROS DE INTERÉS PARA MATEMÁTICAS DE 2º DE BACHILLERATO: PRUEBA DE ANÁLISIS Y ÁLGEBRA DE MATRICES PARA 2º BACHILLERATO
EJERCICIO M2BE2421:
Calcula los valores de los parámetros a, b ∈ ℜ para que la función f(x) = (x2-a) ex + bx tenga un punto de inflexión en x = 0 y un mínimo relativo en x = 1.
IR AL ARTÍCULO QUE CONTIENE LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES, ÁLGEBRA, GEOMETRÍA ESPACIAL Y PROBABILIDAD PARA MATEMÁTICAS II DE 2º BACHILLERATO
EJERCICIO M2BE2213:
El propietario de una empresa ha estimado que si compra «x» máquinas y contrata «y» empleados, el número de unidades de producto que podría fabricar vendría dado por la función f(x, y) = 9xy2. Sabiendo que tiene un presupuesto de 22500 €, que cada máquina supone una inversión de 2500 € y cada contrato de un nuevo empleado 1 500 €, determine el número de obreros que debe contratar y el número de máquinas que debe comprar para optimizar la producción.
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO QUE ESTÁ INCLUÍDO EN UNA PRUEBA DE EXAMEN GLOBAL PARA MATEMÁTICAS II DE 2º DE BACHILLERATO: EXAMEN GLOBAL MATEMÁTICAS II 2º BACHILLERATO. GEOMETRÍA, ÁLGEBRA DE MATRICES, PROBABILIDAD, ANÁLISIS (OPTIMIZACIÓN)
EJERCICIO M2BE2223:
Se dispone de una barra de hierro de 10 metros para construir una portería, de manera que la portería tenga la máxima superficie interior posible.
¿Qué longitud deben tener los postes y el larguero?
EJERCICIO M2BE2272 EBAU CANARIAS JUNIO 2023:
Se quiere construir una Casa de la Juventud de 240 m2 de superficie, que estará rodeada por una zona ajardinada con las dimensiones de la imagen.
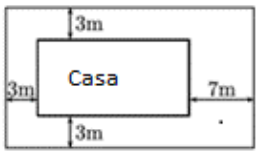
Si se quiere minimizar la superficie total de la zona ajardinada, ¿qué dimensiones debe tener la Casa de la Juventud? ¿Cuál es el área de la zona ajardinada?.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE PROBLEMA DE OPTIMIZACIÓN: MATEMÁTICAS II. E.B.AU. CANARIAS 2023. EJERCICIOS RESUELTOS. CONVOCATORIA ORDINARIA JUNIO
EJERCICIO M2BE2287:
Se desea vallar un terreno rectangular usando 100 m de una tela metálica. Se ha decidido dejar una abertura de 20 m sin vallar en uno de los lados de la parcela para colocar una puerta.
Calcular las dimensiones de todos los lados de la parcela rectangular de área máxima que puede vallarse de esa manera. Calcular el valor de dicha área máxima.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE OPTIMIZACIÓN
EJERCICIO M2BE2333:
Obtener la ecuación de la recta tangente y la recta normal a la curva f(x) = Ln ((x+1)/(x-1)), en el punto de abscisa x=3
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/GRbly7emcLk
EJERCICIOM2BE2930:
Consideremos la siguiente función:

donde L𝑛 denota el logaritmo neperiano. Resuelva justificadamente los siguientes apartados:
a) El dominio, los intervalos de crecimiento y decrecimiento, así como los posibles extremos relativos de la función .
b) La ecuación de la recta tangente a f(x) en x=10.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25
EJERCICIOM2BE2952:
Determinar una función de la forma f(x) = x3 + ax2 + bx + c , que tenga un extremo relativo en el punto de abscisa x = 2 y para la cual el punto sea un punto de inflexión.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25
PODRÍA INTERESAR VISITAR LOS SIGUIENTES ENLACES RELACIONADOS:
- CURSO DE CÁLCULO DE DERIVADAS PARA BACHILLERATO
- CÁLCULO DE DERIVADAS PARA MATEMÁTICAS DE BACHILLERATO
- FUNCIONES: LÍMITES, DERIVADAS Y APLICACIONES
- DERIVADAS EN FÍSICA
- APLICACIONES DE LA DERIVADA PARA MATEMÁTICAS DE 2º DE BACHILLERATO
DOCUMENTO CON CLAVES Y EJERCICIOS PROPUESTOS DE CÁLCULO DE PARÁMETROS:
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN:
