EJERCICIOS ANÁLISIS FUNCIONES BACHILLERATO
EJERCICIOS DE ANÁLISIS DE FUNCIONES PARA BACHILLERATO, LÍMITES DERIVADAS Y APLICACIONES:

PUEDE INTERESAR LA CONSULTA DE:
-
- FUNCIONES: ANÁLISIS PARA BACHILLERATO
- PROPIEDADES DE LOS LÍMITES DE FUNCIONES
- LÍMITES PARA MATEMÁTICAS DE BACHILLERATO
- LÍMITES: USO DEL NÚMERO «e» PARA RESOLVER INDETERMINACIONES
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- ASÍNTOTAS VERTICALES, HORIZONTALES Y OBLÍCUAS. RAMAS PARABÓLICAS: APLICACIONES DE LOS LÍMITES DE FUNCIONES
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- ESTUDIO DE LA DERIVABILIDAD DE UNA FUNCIÓN
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA:
ASPECTOS FORMALES LOMLOE AL FINAL DEL ARTÍCULO
EJERCICIO M2BE2602:
Calcula los parámetros a y b para que la función definida a continuación sea derivable en todo ℜ.

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II, 2º BACHILLERATO. ANÁLISIS DE FUNCIONES. PRUEBA 1 DEL PRIMER TRIMESTRE DEL CURSO 25-26
EJERCICIO M2BE2355:
Considera la función f(x) = ax3 + bx2 + cx + d.
Calcular los coeficientes a, b, c y d, sabiendo que f tiene un extremo relativo en el punto P(0,1) y su gráfica tiene un punto de inflexión Q(1, -1).
Dar la expresión de la función f(x).
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II, 2º BACHILLERATO. ANÁLISIS DE FUNCIONES. PRUEBA 1 DEL PRIMER TRIMESTRE DEL CURSO 25-26
EJERCICIO M2BE2017:
Dada la función:
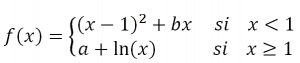
a.- Estudia los valores de los parámetros a y b para que la función f(x) sea continua y derivable en ℜ. Escribe la función resultante f(x).
b.- Tomando los valores a=-2 y b=1, calcula la ecuación de la recta tangente en x=e.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/foUIAm2GnC4
EJERCICIO M2BE2124:
Sea la función f(x) = 1 + 1/x ,
a.- Determinar el dominio y los intervalos de crecimiento y de decrecimiento de la función f(x) (monotonía de la función).
b.- Dada la función g(x) = (5-x)/2 , hallar el área de la región acotada por las gráficas de las funciones f(x) y g(x).
EJERCICIO M2BE2125:
Sea la función f(x) = x3 + cos(πx) . Se pide:
a.- Calcular la recta tangente a la gráfica de f(x) en x=1.
b.- Calcular:
![]()
EJERCICIO M2BE2277:
Dada la siguiente función f(x):
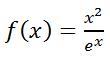
a.- Determinar los intervalos de crecimiento y los de decrecimiento.
b.- Calcular los máximos y mínimos relativos.
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO M2BE3473:
Calcula todas las asíntotas de la función f: ℜ → ℜ:
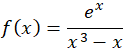
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO BLOQUE DE ANÁLISIS DE FUNCIONES Y ÁLGEBRA (MATRICES Y DETERMINANTES), PARA MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 1 DEL SEGUNDO TRIMESTRE CURSO 2025-26, REALIZADO EN «EL PILAR»
EJERCICIO M2BE3060:
Considera la función f: ℜ→ℜ definida por f(x) = (x – 1) · e x .
a) Determina la ecuación de la recta tangente a la función f(x) en el punto de inflexión.
b) Estudia y calcula las asíntotas de la función. (Tener en cuenta en estos cálculos la opción en la que x tiende a menos infinito).
EJERCICIO M2BE3065:
La profesora Kiara tiene un patio en su casa. El patio está delimitado por las funciones: f(x) = x2 – 4x + 4 y g(x) = – x2 + 2x + 4 . Suponiendo que el gráfico está en metros.
a) Realiza el boceto del patio de la casa de Kiara, obteniendo todos los puntos importantes de las funciones f y g.
b) Kiara va a pintar el patio con pintura antideslizante. El metro cuadrado de patio pintado tiene un coste de 85 euros. Kiara tiene ahorrados 750 euros. ¿Kiara puede costear con sus ahorros el coste del pintado del patio?
EJERCICIO M2BE3061:
Realizar la siguiente integral, argumentando cada paso:

EJERCICIO M2BE3062:
Realizar la siguiente integral, argumentando cada paso:

EJERCICIO M2BE3063:
Realizar la siguiente integral, argumentando cada paso:

EJERCICIO M2BE3064:
Realizar la siguiente integral, argumentando cada paso:
![]()
EJERCICIO M2BE2163, EBAU Canarias 2017:
Se quiere fabricar un smartphone con una pantalla LCD de 18 cm2. Los bordes superior e inferior han de tener 2 cm cada uno y los bordes laterales 1 cm. Calcular las dimensiones del teléfono para que la superficie del mismo sea mínima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/Us6K799tABA
MÁS EJERCICIOS DE ANÁLISIS DE FUNCIONES PARA BACHILLERATO EN:
EJERCICIO M1BE2019:
PLANTEARSE LAS SIGUIENTES PREGUNTAS TIPO TEST:
IR A LAS SOLUCIONES DE LAS PREGUNTAS: SOLUCIONES VARIAS ALUMNOS
EJERCICIOM2BE2930:
Consideremos la siguiente función:

donde L𝑛 denota el logaritmo neperiano. Resuelva justificadamente los siguientes apartados:
a) El dominio, los intervalos de crecimiento y decrecimiento, así como los posibles extremos relativos de la función .
b) La ecuación de la recta tangente a f(x) en x=10.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25
EJERCICIO M2BE3227 (PAU 2025 Convocatoria Extraordinaria-Julio Canarias):
El modelo logístico es un modelo matemático utilizado para describir la evolución de una población a lo largo del tiempo, cuando los recursos son limitados. Es uno de los modelos matemáticos más comunes en biología y describe cómo la población se estabiliza cuando alcanza la capacidad de carga del entorno, esto es, el tamaño máximo que puede alcanzar una población antes de que los recursos se vuelvan insuficientes, lo que genera competencia y, en muchos casos, una desaceleración de la tasa de crecimiento o una crisis en la población.
Un ejemplo de modelo logístico lo encontramos en las colonias de hormigas, que están compuestas por una red de túneles, entradas, cámaras de cría y áreas de almacenamiento, donde las hormigas establecen su hábitat.
Un grupo de investigadores ha estudiado el momento en el que unas hormigas forman una nueva colonia y ha modelizado el número de hormigas (H(t)) después de t meses con la función:
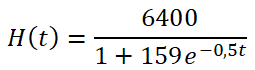
a) ¿Cuántas hormigas formaron la nueva colonia inicialmente?
b) ¿Cuál es la tasa media de crecimiento el primer año? ¿Y el segundo año? Interpretar el resultado.
PARA ESTE APARTADO PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
c) Un observador afirma que el modelo siempre es creciente y entiende que la población de hormigas crece sin control. Justificar matemáticamente si esta afirmación es o no correcta.
d) ¿En qué momento la colonia de hormigas alcanzará la mitad de su capacidad de carga?
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3227 DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO, PARA MATEMÁTICAS DE BACHILLERATO. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3220 (PAU 2025 Convocatoria Ordinaria-Junio Canarias):
En un hospital de las Islas Canarias, un equipo de investigación está analizando cómo se metaboliza en sangre un nuevo medicamento llamado Metabolix, utilizado para tratar infecciones bacterianas. La concentración residual del fármaco en el plasma sanguíneo, denotada como f(x) (medida en miligramos por litro, mg/L), depende del tiempo transcurrido x (en horas) desde su administración. El estudio indica que el medicamento sigue dos fases diferenciadas:
- Fase de absorción: En las primeras dos horas, el fármaco se distribuye por el organismo.
- Fase de eliminación: A partir de la segunda hora, el fármaco empieza a eliminarse.
Este comportamiento se modeliza mediante la siguiente función matemática:
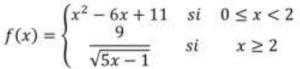
El equipo de investigación necesita aclarar algunas dudas del modelo matemático:
a) Confirmar si este modelo es realmente continuo. Justifica tu respuesta.
b) La concentración residual varía con el tiempo, comprobar que la velocidad de crecimiento instantánea de la concentración residual a las 3 horas de administrar Metabolix es mayor que -0.5 (mg/L)/h.
c) ¿Es cierto que la concentración residual del fármaco en la sangre siempre va disminuyendo con respecto al tiempo transcurrido? Averiguar en qué instante la concentración residual es máxima у calcular el valor de dicha concentración.
d) Pasado un largo periodo de tiempo, ¿cuál será la concentración residual de este medicamento?
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO: EJERCICIO M2BE3220 RESUELTO, CONTEXTUALIZADO DE ANÁLISIS. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE2031:
Realizar el estudio completo de la siguiente función:
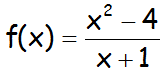
CONTRASTAR LO OBTENIDO ANALÍTICAMENTE CON LA REPRESENTACIÓN GRÁFICA EN GEOGEBRA
EJERCICIO M2BE2032:
Realizar el estudio completo de la siguiente función:
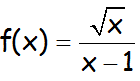
CONTRASTAR LO OBTENIDO ANALÍTICAMENTE CON LA REPRESENTACIÓN GRÁFICA EN GEOGEBRA
SOBRE LA EJECUCIÓN DE ESTE EJERCICIO EN CLASE: Manualmente es terrible la 2ª derivada, pero corresponde a la expresión que se muestra, utilizando la aplicación wiris; que además en la búsqueda del punto de inflexión y al resolver la ecuación correspondiente nos devuelve dos soluciones de las que sólo sirve una, la primera, por estar la otra fuera del dominio. Esta solución válida numéricamente es x=0,1547, que se observa en la representación que efectivamente tiene un punto de inflexión:

EJERCICIO M2BE2002 JL:
Realizar el estudio de las asíntotas horizontales de la siguiente función:
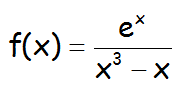
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/mfTP_-Sgen0
EJERCICIO M1BE2018:
Representar la función f(x), haciendo un estudio completo de la misma:
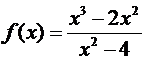
PUEDE INTERESAR CONSULTAR LA SIGUIENTE PRUEBA/EXAMEN RESUELTA DE ESTE CONTENIDO PARA MATEMÁTICAS DE 2º DE BACHILLERATO:
PRUEBA DE ANÁLISIS PARA MATEMÁTICAS DE 2º BACHILLERATO
ASPECTOS FORMALES:
SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:
- COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente el DESCRIPTOR OPERATIVO STEM1.
- COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente el DESCRIPTOR OPERATIVO CCL2.
- COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1.
- COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente el DESCRIPTOR OPERATIVO CPSAA1.1
- COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE1
CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO
MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3
SE OBSERVAN LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS I Y II Y ESTÁN HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE
