INTEGRALES RACIONALES CURIOSAS ARCOTANGENTE
EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES CURIOSAS QUE TERMINAN EN ARCOTANGENTE:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- INTEGRACIÓN DE FUNCIONES RACIONALES
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- EJERCICIOS RESUELTOS DE INTEGRALES POR PARTES
- MÉTODOS DE INTEGRACIÓN PARA INTEGRALES TRIGONOMÉTRICAS
- MÉTODO DE INTEGRACIÓN PARA INTEGRALES IRRACIONALES. CÁLCULO INTEGRAL
SIGUE EL PROCESO DETERMINADO POR:
Y puede formar parte de: AYUDANDO A NUESTROS ALUMNOS QUE ESTÁN EN LA UNIVERSIDAD
En este artículo intentamos ayudar a visualizar como determinadas expresiones polinómicas de 2º grado podemos llevarlas a identidades notables incompletas, que posteriormente se podrán integrar con la estrategia de la arcotangente.
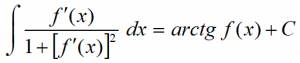
Todos sabemos que:
(x + 1)2 = x2 + 2x + 1
Con lo que si tenemos: x2 + 2x + 2 , podemos expresarlo como: (x + 1)2 + 1
Complicando algo más las cosas, si nos encontramos con:
x2 + x + 1 , debemos caer en la cuenta que el término de primer grado nos obliga a pensar en una expresión del tipo: (x + 1/2)2 , ya que:
(x + 1/2)2 = x2 + 2x·1/2 + 1/4 = x2 + x + 1/4
como encima el término independiente debe ser 1, pues tendremos que sumar otros 3/4. Por ello:
x2 + x + 1 = (x + 1/2)2 + 3/4
Lo que no resulta nada sencillo de obtener o razonar.
Del mismo modo, debemos ser capaces de ver que:
x2 – 4x + 9 = (x – 2)2 + 5
ya que (x – 2)2 = x2 – 4x + 4
Al igual que:
x2 – 4x + 5 = (x – 2)2 + 1
O incluso, mucho más complicado:
x2 + 3x + 1 = (x + 3/2)2 – 5/4 ;
que aunque está bien, no sirve para hacer la integral arcotangente, ya que sólo es posible cuando la estructura es: (algo) 2+ algo
Ya que (x + 3/2)2 = x2 + 3x + 9/4
O este otro:
x2 – 3x + 3 = (x – 3/2)2 + 3/4
Ya que (x – 3/2)2 = x2 – 3x + 9/4
EJERCICIO M2BE3348: (Ejercicio 25-d relación 1 de integrales indefinidas)
Resolver la siguiente integral indefinida:
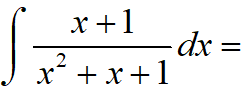
RESOLUCIÓN DE LA INTEGRAL:
EJERCICIO M2BE3350:
Resolver la siguiente integral indefinida:
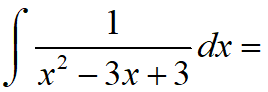
RESOLUCIÓN DE LA INTEGRAL:
EJERCICIO M2BE117A:
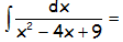
RESOLUCIÓN DE ESTA INTEGRAL:
DE OTRO MODO: IR AL ARTÍCULO CON LA RESOLUCIÓN DE LA INTEGRAL TRATÁNDOLA COMO UNA INTEGRAL RACIONAL DE DENOMINADOR CON RAÍCES IMAGINARIAS: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES
EJERCICIO M2BE117C:
Resolver la siguiente integral indefinida:
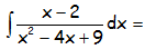
IR AL ARTÍCULO CON LA RESOLUCIÓN DE LA INTEGRAL TREMENDAMENTE SENCILLA: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES
EJERCICIO M2BE118C:
Resolver la siguiente integral indefinida:
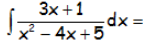
IR AL ARTÍCULO CON LA RESOLUCIÓN DE LA INTEGRAL TRATÁNDOLA COMO UNA INTEGRAL RACIONAL DE DENOMINADOR CON RAÍCES IMAGINARIAS: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES


