FLIPPED SUMMER CLASSROOM MATEMÁTICAS

PARA QUE FLIPPES CUANDO INICIES 2º DE BACHILLERATO EN MATEMÁTICAS:

PARA QUE INICIES UN CURSO MUY COMPLEJO COMO UNA MOTO Y CONSIGAS LOS RESULTADOS ESPERADOS SIN ESTRÉS.

A FAVOR DE UN VERANO INVERTIDO.

A nadie se le escapa que 2º de bachillerato es un curso complejo y definitivo. Dura menos, tenemos la EBAU a la vista y los que llevamos como mínimo un par de décadas dando clases en este curso, primero COU y después 2º de Bachillerato, sabemos que se atraganta, o cuanto menos, cuesta conseguir los objetivos esperados, sobre todo si son muy ambiciosos. Además los alumnos y las familias «sufren» un curso muy especial…. quién lo ha vivido… lo sabe.

Desde el proyecto Achimagec queremos ayudar a nuestros alumnos a que consigan sus objetivos en 2º de bachillerato en lo que se refiere a MATEMÁTICAS, FÍSICA Y QUÍMICA, al menos. Eso sí, comprometiendo algo del tiempo de ocio, con un poco de trabajo y esfuerzo.

En este artículo vamos a ir poniendo materiales audiovisuales, propios de dinámicas Flipped Classroom (CLASE INVERTIDA), que el alumno pueda relajadamente ver en verano (de ahí lo de FLIPPED SUMMER) y que entendemos que van a suponer una introducción a los contenidos de 2º de Bachillerato, con el magnífico objetivo de que desde el primer día de clase, se puedan seguir las explicaciones con éxito. Tengan en cuenta que en verano también hay tiempo para todo… y seamos sinceros… a veces, en verano, hasta nos aburrimos.

Estos materiales intentaremos que sean asequibles para el alumno con los contenidos vistos en primero de bachillerato y que si no tienen nada que ver con lo visto en primero de bachillerato, se puedan entender sin grandes esfuerzos.

Por las características de la dinámica, va dirigida a los alumnos de 1º de Bachillerato que han aprobado sus asignaturas y tienen el verano libre. Entendemos que si tenemos que estudiar algo para prueba extraordinaria, ésa debe ser la prioridad. En cualquier caso nuestro ánimo para los que tienen que acudir a prueba extraordinaria y que sepan que no pasa nada, porque el curso termina en septiembre.

Si ése fuera el caso y el alumno tiene que acudir a prueba extraordinaria de Matemáticas o Física y Química, le recomendamos los siguientes materiales apropiados:

PRUEBA EXTRAORDINARIA MATEMÁTICAS I, 1º BACHILLERATO

PRUEBA EXTRAORDINARIA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO

Pretendemos con esta dinámica, que supone una «no desconexión» de lo académico en los dos meses y medio de vacaciones, que el alumno suba sus expectativas, obtenga los resultados esperados y sobre todo baje su nivel de ansiedad cuando se encuentre en 2º de bachillerato, desde el primer día de clase.

En verano se producen dos fenómenos neuro-psicológicos alternativos, consecutivos o simultáneos dependiendo del caso: o el cerebro se congela, o se derrite, dependiendo de la latitud. Esta situación se observará, como sabemos todos, en docentes y alumnos, los primeros días de clase del curso que está por venir. Con esta dinámica pretendemos también mantener el cerebro a la temperatura óptima de trabajo durante todo el año natural.

Entendemos además que los alumnos que se acojan a esta experiencia deberían comunicarlo a sus profesores al inicio del curso, ya que ser un «Flippado» que aprovecha también el verano para conseguir sus objetivos, merece cuando menos una felicitación por parte del docente y un reconocimiento por parte de todos. Ni que decir tiene que la familia del alumno «flippado» debería tener en cuenta este comportamiento positivo y aumentar los privilegios familiares del alumno.

Esta iniciativa debe valorarse en el contexto que marcan los siguientes artículos:

CETERIS PARIBUS, UNA PROPUESTA DE TUTORÍA PARA 2º DE BACHILLERATO

TENER ÉXITO EN FÍSICA Y QUÍMICA Y MATEMÁTICAS

SENTIDO DE INICIATIVA Y ESPÍRITU EMPRENDEDOR: EL MÉTODO B.L.V.

Intentaremos organizar este artículo, en construcción, en tres categorías diferentes:

  • CONTENIDOS QUE SE HAN TRABAJADO EN PRIMERO DE BACHILLERATO QUE SIRVEN PARA 2º DE BACHILLERATO.
    • Nos referiremos aquí a contenidos como Análisis de Funciones (derivadas, límites y sus aplicaciones)
  • CONTENIDOS QUE TRABAJADOS EN 1º DE BACHILLERATO SON UNA BASE INESTIMABLE PARA 2º DE BACHILLERATO, AUNQUE EN 2º Y EN EBAU SE TRATAN A OTRO NIVEL SUPERIOR.
    • Como Geometría en 2D, que es la base de la Geometría 3D para 2º de Bachillerato
  • CONTENIDOS NUEVOS ACCESIBLES PARA EL ALUMNO «FLIPPADO».
    • El mejor ejemplo es Probabilidad, que aparte de sencillo tiene un puntito interesante. Como ejemplo, esta cuestión:
      • «La probabilidad de que un alumno flippado aumente un 20% su nota en 2º de bachillerato es de 0,85. Hallar la probabilidad de que de 8 alumnos flippados elegidos al azar, dos de ellos no aumenten su nota un 20%.»  (SOLUCIÓN: 0,2376)

 

CONTENIDOS QUE SE HAN TRABAJADO EN PRIMERO DE BACHILLERATO QUE SIRVEN PARA 2º DE BACHILLERATO:

Recomendables sin ninguna duda los ejercicios que tienen videos de los artículos siguientes:

 

Resolución de sistemas de ecuaciones utilizando la regla de Cramer.

EJERCICIO M2BE1958:

Resolver el siguiente sistema de ecuaciones, utilizando la regla de Cramer:

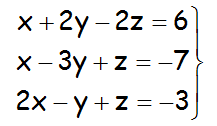
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/9FYjSgcr-XM

CONTENIDOS QUE TRABAJADOS EN 1º DE BACHILLERATO SON UNA BASE INESTIMABLE PARA 2º DE BACHILLERATO, AUNQUE EN 2º Y EN EBAU SE TRATAN A OTRO NIVEL SUPERIOR.

Recomendamos los videos del siguiente enlace de GEOMETRÍA PLANA:

Creemos además que con los conocimientos de geometría plana vistos en el enlace anterior, pueden dar el salto a geometría 3D del siguiente ejercicio:

EJERCICIO M2BE2001 JL, de conceptos básicos de geometría en el espacio (Puntos, vectores, módulo del vector=distancia entre dos puntos):

Considerando los puntos  A (4,5,3) y B (2,1,4), obtener:

a.- El vector AB y el vector BA

b.- El módulo de cada uno de esos vectores, que coincidirá con la distancia que separa los dos puntos.

IR AL VIDEO QUE RESUELVE EL EJERCICIO, DE FORMA ANALÍTICA Y A TRAVÉS DEL USO DE GEOGEBRA EN 3D PARA IPAD: https://youtu.be/DoETyRo4UXw

 

CONTENIDOS NUEVOS ACCESIBLES PARA EL ALUMNO «FLIPPADO».

Sugerimos para el contenido de PROBABILIDAD, la visualización de los videos del siguiente enlace, comenzando por los de la ficha 1, y por orden. Esos materiales se encuentral al final del artículo:

EJERCICIO M2BE2003 JL:

Una estación de medición de calidad del aire mide niveles de dióxido de nitrógeno y de partículas en suspensión. La probabilidad de que en un día se mida un nivel de dióxido de nitrógeno superior al permitido es 0.16. En los días en los que se supera el nivel permitido de dióxido de nitrógeno, la probabilidad de que se supere el nivel permitido de partículas es 0.33. En los días en los que no se supera el nivel permitido de dióxido de nitrógeno, la probabilidad de que se supere el nivel permitido de partículas es 0.08.

a) ¿Cuál es la probabilidad de que en un día se superen los dos niveles permitidos?

b) ¿Cuál es la probabilidad de que se supere al menos uno de los dos niveles permitidos?

c) ¿Son independientes los sucesos A = en un día se supera el nivel permitido de dióxido de nitrógeno y B = en un día se supera el nivel permitido de partículas?

d) ¿Cuál es la probabilidad de que en un día se supere el nivel permitido de dióxido de nitrógeno, sabiendo que no se ha superado el nivel permitido de partículas?

IR AL VIDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/QUL-dlueuOs

EJERCICIO M2BE2022 (EBAU CANARIAS JUNIO 2022):

Tenemos una caja con bolas de madera y de plástico de distintos colores, pero con el mismo tamaño y aspecto. Contamos con la siguiente información de su contenido:

– El 38% son bolas azules y, de este color, la mitad son de madera.
– El 29% son bolas rojas y, de este color, las tres cuartas partes son de madera.
– El 33% son bolas verdes y, de este color, dos tercios son de madera.

Extraemos una bola de la caja. Responde a las siguientes preguntas:

a) Construye el árbol de probabilidades.
b) Calcula la probabilidad de que, al sacar una bola al azar de la caja, esta sea de madera.
c) Si la bola extraída de la caja es de plástico, ¿qué probabilidad hay de que sea de color rojo?.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/o9asBVVTRzc

…. estamos trabajando en esta línea… no olvides recargar la página frecuentemente.

Post Views: 1.458
On:

Comments are closed, but trackbacks and pingbacks are open.