PREPARACIÓN EXTRAORDINARIA MATEMÁTICAS II
EJERCICIOS PREPARACIÓN PRUEBA EXTRAORDINARIA MATEMÁTICAS II, 2º BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE:
-
- FUNCIONES: ANÁLISIS PARA BACHILLERATO
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- MATRICES Y DETERMINANTES PARA BACHILLERATO.
- RESOLUCIÓN DE ECUACIONES Y SISTEMAS DE ECUACIONES MATRICIALES
- DISCUSIÓN Y RESOLUCIÓN DE SISTEMAS LINEALES. ROUCHÉ Y CRAMER
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- PROBABILIDAD. DIAGRAMAS EN ÁRBOL.
- DISTRIBUCIÓN BINOMIAL DE PROBABILIDAD, PARA MATEMÁTICAS DE BACHILLERATO
- DISTRIBUCIÓN NORMAL DE PROBABILIDADES, PARA MATEMÁTICAS DE BACHILLERATO
SE RECOMIENDA LA CONSULTA DE LOS SIGUIENTES MATERIALES: EXÁMENES RESUELTOS DE MATEMÁTICAS II DE 2º DE BACHILLERATO REALIZADOS EN «EL PILAR»
ESTA RELACIÓN DE EJERCICIOS SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
EJERCICIO M2BE2224:
En el armario de las llaves, hay tres llaveros: uno de ellos tiene 5 llaves, 2 de ellas abren la nevera, el segundo llavero consta de 8 llaves y 3 de las llaves abren la nevera, y el tercer llavero, tiene 15 llaves y solo 1 abre la nevera.
Una persona al azar coge un llavero, y también al azar, una llave de ese llavero e intenta abrir la nevera.
A) Calcular la probabilidad de que no abra la puerta de la nevera.
B) Calcular la probabilidad de que elija el llavero dos y abra la nevera.
C) Si la puerta de la nevera se abrió, calcular la probabilidad de que fuera con el llavero uno.
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO M2BE2224 DE PROBABILIDAD. DIAGRAMAS EN ÁRBOL. MATEMÁTICAS BACHILLERATO
EJERCICIO M2BE2225: EBAU CANARIAS 2011
Dadas las funciones: y = – x2 + 4x e y = 2x2 – 2x
a.- Representar la región que determinan sus gráficas.
b.- Calcular el área de dicha región.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2226: EBAU CANARIAS 2012
Calcular la matriz X tal que X · A + 3B = 2C , siendo:
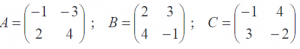
(detallar todos los cálculos realizados).
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2226 DE ECUACIONES MATRICIALES. EBAU CANARIAS 2012
EJERCICIO M2BE2227:
Calcula los intervalos de crecimiento-decrecimiento y los máximos-mínimos de la función,
f(x) = (x2+3x+1) · e-x
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2227 DE APLICACIONES DE LA DERIVADA: MONOTONÍA (INTERVALOS DE CRECIMIENTO Y DECRECIMIENTO), EXTREMOS Y CURVATURA.
EJERCICIO M2BE2228:
Sea el punto P (0,-1,2) y la recta r determinada por:
![]()
a.- Calcula la forma general del plano π que contiene a la recta r y al punto P.
b.- Calcula la recta s, perpendicular al plano π, que pasa por el punto medio A(1,0,-1) y B(-1,-2,-1)
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO DE GEOMETRÍA EN EL ESPACIO. ECUACIONES DE RECTAS Y PLANOS.
EJERCICIO M2BE2229:
Considera el siguiente sistema de ecuaciones:
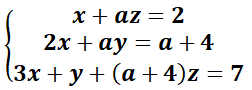
a.- Discute el sistema según los valores de a.
b.- Resuelve el sistema para a=2.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN FINAL RESUELTO DE MATEMÁTICAS II, DE 2º BACHILLERATO. MAYO 2025
EJERCICIO M2BE2956:
¿Cuándo la matriz A es regular (tiene inversa)? Si es posible, realiza la inversa para m=2.
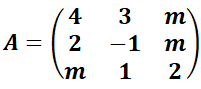
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25
EJERCICIO M2BE2485:
Según datos recogidos por el Instituto Nacional de Estadística, el sueldo mensual de las personas entre 25 y 35 años en la ciudad de Las Palmas de G.C. sigue una distribución normal, de media 950 € y varianza 900 €2. En el periódico LA CICER, se publica el siguiente titular:
«Menos del 5% de las personas entre 25 y 35 años en Las Palmas de Gran Canaria cobra más de 1000 euros mensuales.»
¿Es cierto el titular? Argumenta la respuesta.
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXAMEN FINAL RESUELTO DE MATEMÁTICAS II, DE 2º BACHILLERATO. MAYO 2025
EJERCICIO M2BE3151, 2486m:
En un estudio, se obtiene que el setenta y cinco por ciento de las entradas para un concierto del grupo de rock Los Albertos, se realizan a través de internet.
a) En una muestra elegida al azar de 8 personas, ¿qué probabilidad hay de que más de 3 entradas se compraran a través de internet?
b) En una muestra elegida al azar de 80 personas, ¿qué probabilidad hay de que más de 65 entradas se compraran a través de internet?
IR AL ARTÍCULO QUE CONTIENE LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN FINAL RESUELTO DE MATEMÁTICAS II, DE 2º BACHILLERATO. MAYO 2025
EJERCICIO M2BE2233: EBAU CANARIAS JUNIO 2003
Se sospecha que el plano definido por el punto (1, 0, 5) y los vectores u = (3, 1, 1), v = (-1, 3, -2) se corta en un punto con la recta cuyas ecuaciones en forma continua son:
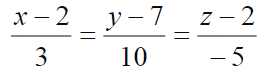
Decidir razonadamente la cuestión.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE2233 RESUELTO DE GEOMETRÍA ESPACIAL PARA BACHILLERATO. POSICIÓN RELATIVA DE PLANO Y RECTA. EBAU CANARIAS JUNIO 2003
EJERCICIO M2BE2234:
Hallar el área (representándola previamente) del recinto determinado por las funciones f(x) = 2√x y g(x) = x.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2234 DE CÁLCULO DE ÁREAS LIMITADAS POR FUNCIONES. APLICACIÓN DE LA INTEGRAL DEFINIDA
EJERCICIO M2BE2235:
Hallar el área limitada por las gráficas de las funciones: y=ln x , y=1 y los ejes de coordenadas. Realizar una representación de la situación.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2235 DE CÁLCULO DE ÁREAS LIMITADAS POR FUNCIONES. APLICACIÓN DE LA INTEGRAL DEFINIDA
EJERCICIO M2BE2236:
Una prueba rápida para detectar una enfermedad da un 2% de falsos positivos (personas sanas en las que la prueba da positivo, clasificándolas como enfermas) y un 1% de falsos negativos (personas enfermas en las que la prueba da negativo, clasificándolas como sanas). En una población hay un 4% de enfermos.
a) Calcule la probabilidad de que el test dé un resultado negativo.
b) La prueba da un resultado positivo (clasificando a la persona como enferma). Calcule la probabilidad de que realmente esté sana.
SOLUCIONES: P(-)=0,96·0,98+0,04·0,01=0,9412; P(S/+)=0,3265
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO M2BE2236 RESUELTO DE PROBABILIDAD, DIAGRAMA EN ÁRBOL. FALSOS POSITIVOS
EJERCICIO M2BE2237:
Un estudio ha mostrado que, en un cierto barrio, el 60% de los hogares tienen al menos dos coches. Se elige al azar una muestra de 50 hogares en el citado barrio.
a.- ¿Cuál es la probabilidad de que al menos 20 de los citados hogares tengan cuando menos dos coches?
b.- ¿Cuál es la probabilidad de que entre 30 y 40 hogares, ambos incluidos, tengan al menos dos coches?
EJERCICIO M2BE2238: EBAU CANARIAS JULIO 2017
Sea M la siguiente matriz:
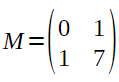
Resolver el siguiente sistema de ecuaciones matriciales:
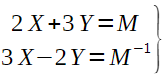
EJERCICIO M2BE2239: EBAU CANARIAS JUNIO 2013
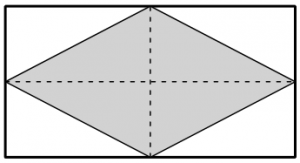
La figura siguiente muestra un rombo inscrito dentro de un rectángulo, de forma que los vértices del rombo se sitúan en los puntos medios de los lados del rectángulo. El perímetro del rectángulo es de 100 metros. Calcular las longitudes de sus lados para que el área del rombo inscrito sea máxima.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2239, PROBLEMA DE OPTIMIZACIÓN EBAU CANARIAS JUNIO 2013
EJERCICIO M2BE2240: EBAU CANARIAS JULIO 2013
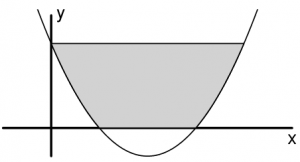
La siguiente gráfica corresponde a la función f(x) = x2 – 4x + 3 representada respecto a los ejes coordenados. Calcular el área de la parte sombreada.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2240 DE CÁLCULO DE ÁREAS LIMITADAS POR FUNCIONES. APLICACIÓN DE LA INTEGRAL DEFINIDA. EBAU CANARIAS JULIO 2013
EJERCICIO M2BE2241: EBAU CANARIAS JULIO 2013
Dada la matriz siguiente:
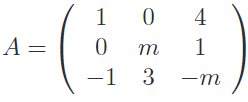
a.- Determinar los valores del parámetro m para los que la matriz A tiene inversa.
b.- Calcular la inversa de la matriz A para m=2.
EJERCICIO M2BE2242: EBAU CANARIAS JULIO 2013:
Dadas las rectas:

a.- Determinar la ecuación general del plano paralelo a las rectas r y s y que pasa por el origen de coordenas.
b.- Hallar el ángulo que forman r y s.
EJERCICIO M2BE2243: EBAU CANARIAS JULIO 2013
Dado el siguiente sistema de ecuaciones:
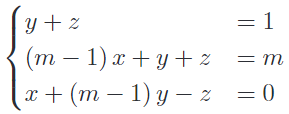
a.- Discutirlo según los valores de m.
b.- Resolverlo para m=2.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO M2BE2243 DE DISCUSIÓN DE SISTEMAS EN FUNCIÓN DE UN PARÁMETRO A TRAVÉS DEL TEOREMA DE ROUCHÉ. EBAU CANARIAS JULIO 2013
EJERCICIO M2BE2244: EBAU CANARIAS JUNIO 2014
Dados los puntos A (-1,0,3), B (2,4,1) y C (-4,3,1):
a.- Estudiar si los puntos A,B y C están alineados.
b.- Hallar la ecuación de la recta paralela al segmento AB y que pasa por C. Expresarla como intersección de dos planos.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2245:
Dada la matriz A siguiente:
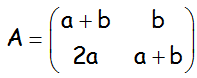
a.- ¿Para qué valores de a y b la matriz A no tiene inversa?
b.- Determinar la matriz inversa para el resto de valores.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2245 DE OBTENCIÓN DE LA MATRIZ INVERSA
EJERCICIO M2BE2246:
Estudiar la posición relativa de los 3 planos siguientes:
2x + 3y – 5z + 1 = 0
x + 2y – z + 12 = 0
4x + 7y – 7z + 5 = 0
EJERCICIO M2BE2247:
Dados los puntos A(-1,0,3), B(2,4,1) y C(-4,3,1).
a.- Obtener la ecuación del plano perpendicular a la recta AB que pasa por el punto simétrico de A con respecto de C.
b.- Calcular la ecuación del plano que pasa por los tres puntos dados.
EJERCICIO M2BE2248:
Dada la siguiente función f(x):
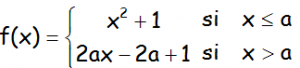
a.- Estudiar para qué valores de a la función es continua.
b.- ¿En algún caso la función es derivable?
EJERCICIO M2BE2249:
Dada la función f(x) = ex (x3 – 4x2 + 7x – 6)
a.- Indicar su dominio.
b.- Estudiar la monotonía de f(x).
c.- Hallar sus extremos relativos.
EJERCICIO M2BE2250:
Tres de cada cinco alumnos de segundo de bachillerato de una región están matriculados en la asignatura de Matemáticas II. Se eligen 6 alumnos al azar entre todos los alumnos de segundo de bachillerato.
a) Calcular la probabilidad de que exactamente cuatro de ellos estén matriculados en Matemáticas II.
b) Es cierta la siguiente afirmación: El porcentaje de que alguno de ellos esté matriculado en Matemáticas II es superior al 99%.
c) Si en un instituto de esa región hay matriculados en segundo de bachillerato 120 alumnos, calcular la probabilidad de que más de 60 de estos alumnos estén matriculados en Matemáticas II.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2251:
El diámetro de las cerezas picotas del Jerte se distribuye normalmente con media de 2,5 cm y desviación típica 2 mm.
a) Se toma una cereza al azar. ¿Cuál es la probabilidad de que tenga un diámetro entre 2,2 cm y 2,8 cm?
b) Si durante la mañana, se han recogida 30200 cerezas. ¿Cuántas se esperan que midan más de 2.75 cm de diámetro?
EJERCICIO M2BE2252:
Dado el plano π ≡ x – y + z = 0
a) Halle el punto simétrico del punto P (1, 0, 1) respecto de π.
b) Halle la posición relativa de la recta que pasa por P y por Q (2, 3, -4) y el plano .
Si fueran secantes, calcular el punto de corte y el ángulo que forman.
EJERCICIO M2BE2253:
Dada la recta r siguiente:
![]()
a.- Hallar la ecuación de la recta s que corta perpendicularmente a r y pasa por el punto A(1, −1, 1).
b.- Calcular el punto P intersección de r y s.
EJERCICIO M2BE2254:
a.- Dibuje el recinto del primer cuadrante limitado por las gráficas de las funciones:
![]()
b.- Calcular el área del recinto delimitado por las tres funciones anteriores.
EJERCICIO M2BE2255:
Se considera la función:
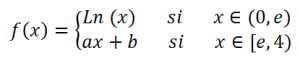
donde a y b son números reales.
Encuentre el valor de a y de b para que la función sea continua y derivable en el intervalo (0,4).
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2256:
Un conocido defraudador fiscal tiene distribuido su dinero negro en tres paraísos fiscales, las Islas Caimán, Panamá y Fiji.
La suma total de este dinero es de 150 millones de euros. Si perdiera la cuarta parte del dinero que tiene en las Islas Caimán, seguiría teniendo allí el triple del dinero que tiene en Panamá. Además, el dinero que tiene en Panamá sumado a las dos quintas partes del dinero que tiene en Fiji es exactamente la mitad del dinero que tiene en las Islas Caimán.
Calcule cuánto dinero tiene en cada uno de los paraísos fiscales.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2257:
En una estantería de una biblioteca hay ensayos, novelas y biografías. Tres de cada dieciséis libros de la estantería son ensayos. Las biografías junto con la tercera parte de los ensayos exceden en dos a las novelas. Si se retiraran la mitad de los ensayos y la quinta parte de las novelas quedarían ciento cinco libros.
Calcule el número de libros de cada clase que hay en la estantería.
IR AL ARTÍCULO QUE RESUELVE EL EJERCICIO: EJERCICIO RESUELTO DE SISTEMA DE ECUACIONES LINEALES 3X3 CONTEXTUALIZADO, CON CIERTA COMPLICACIÓN. REGLA DE CRAMER
EJERCICIO M2BE2267: EBAU CANARIAS 2020
Consideremos la recta r siguiente:
![]()
y el plano π1 ≡ x – y + 3z = 12
a.- Calcular la ecuación del plano π2 que contiene a la recta r y es perpendicular al plano π1.
b.- Sabiendo que la recta r corta al plano π1, averigüe el punto de intersección,
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2382: EBAU CANARIAS 2019
Hallar la ecuación de la recta que verifica simultáneamente las siguientes condiciones:
- Es paralela a los planos de ecuaciones: π1 ≡ x – 3y + z = 0 y π2 ≡ 2x – y + 3z = 5
- Pasa por el punto P (2,-1,5)
EJERCICIO M2BE2259:
Se considera la matriz:
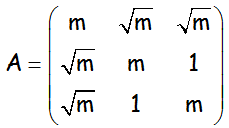
a.- ¿Para qué valores de m tiene inversa la matriz A?
b.- Para m=4 resolver, si es posible, la ecuación matricial AX = 12 I , donde I es la matriz identidad de orden 3.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2260:
La suma de las edades de Carmela, Esperanza y Aurora es 68 años. La edad de Carmela es 5 años más que la mitad de la suma de las edades de Esperanza y Aurora. Además, dentro de 4 años la edad de Aurora será la edad que actualmente tiene Esperanza. Calcular las edades de cada una de ellas.
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: SOLUCIONES DE LOS EJERCICIOS DE SISTEMAS DE ECUACIONES LINEALES (3X3) CONTEXTUALIZADOS. MATEMÁTICAS BACHILLERATO
EJERCICIO M2BE2261:
Una empresa comercializa tres tipos de productos A, B y C. Cuatro de cada siete productos son de tipo A, dos de cada siete productos son de tipo B y el resto lo son de tipo C. A la exportación se destina un 40% de los productos tipo A, un 60% de los productos tipo B y un 20% de los productos tipo C. Se elige al azar un producto. se pide:
- Calcular la probabilidad de que el producto sea destinado a la exportación.
- Calcular la probabilidad de que sea del tipo C sabiendo que el producto es destinado a la exportación.
EJERCICIO M2BE2262:
El 10% de la población de Canarias tiene alergia a la flor del olivo.
- En una muestra de 100 individuos, ¿qué probabilidad hay de que más de 12 seleccionados tengan alergia a la flor del olivo?
- Se toma una muestra de 400 individuos, ¿cuál es la probabilidad de que menos de 32 seleccionados tengan alergia a la flor del olivo?
- En una muestra de 500 individuos, ¿cuál es el número esperado de individuos que no tendrán alergia a la flor del olivo?
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2263:
Se dispone de tres urnas, la urna A contiene 4 bolas rojas y 2 bolas negras, la urna B contiene 3 bolas rojas y 3 bolas negras, y la urna C contiene 6 bolas negras. Se escoge una urna al azar y se extraen dos bolas de manera consecutiva y sin reemplazamiento.
- Calcule la probabilidad de que la primera bola extraída sea roja.
- Calcule la probabilidad de que la primera bola extraída sea roja y la segunda sea negra.
- Sabiendo que la primera bola extraída es roja, calcule la probabilidad de la segunda sea negra.
